最近看了一些代码,忽然发现double类型的数据可表示的范围比long类型的数据表示的范围要大的多,同样是占用64位大小,差距竟如此之大。后来发现,工作了两三年,竟然现在还不太熟悉计算机中浮点数的表示方式,确实有些惭愧。
下面的内容参考自《深入理解计算机系统(原书第三版)》。
IEEE 浮点表示
IEEE浮点标准用 $V=(-1)^s\times M\times 2^E$ 来表示一个数:
- 符号(sign):$s$ 决定是负数($s=1$)还是正数($s=0$);
- 尾数(significand):$M$ 是一个二进制小数,它的范围是$1\thicksim 2-\varepsilon$,或者是$0\thicksim 1-\varepsilon$;
- 阶码(exponent):$E$ 代表2的次幂(可能是负数)。
在计算机中,把浮点数的位表示划分为3段:
- 一个单独的符号位 $s$;
- $k$ 位的阶码字段 $exp=e_{k-1}\cdots e_1e_0$ 编码阶码 $E$;
- $n$ 位小数字段 $frac=f_{n-1}\cdots f_1f_0$ 编码尾数 $M$,编码出来的值依赖于阶码字段的值是否等于0。
举例来说:
10进制中的 $9.0$ 在二进制中写成 $1001.0$,也就是 $1.001\times 2^3$,按照上面的格式,可以算出 $s=0$, $M=1.001$, $E=3$。
10进制中的 $-9.0$ 在二进制中写成 $-1001.0$ ,也就是 $-1.001\times 2^3$,那么 $s=1$, $M=1.001$, $E=3$。
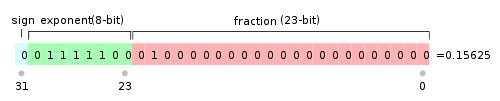
IEEE 754规定,对于32位的浮点数,最高的1位是符号位 $s$,接着的8位是指数 $E$,剩下的23位为有效数字 $M$。
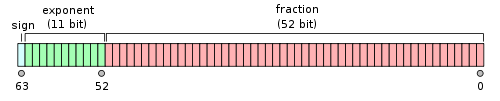
对于64位的浮点数,最高的1位是符号位 $s$,接着的11位是指数 $E$,剩下的52位为有效数字 $M$。
对于上述位的表示,根据阶码 $exp$ 的表示,可以分为三种情况:
规格化的值
这是一般的情况,当 $exp$ 的二进制表示中既不全为0,也不全为1(单精度格式8位,数值为255;双精度格式11位,数值为2047)时,都是这种情况。这种情况下,阶码字段被解释为以偏置(biased)形式表示的有符号整数。也就是说,阶码的值是 $E=e-Bias$,其中 $e$ 是无符号数,其位表示为 $e_{k-1}\cdots e_1e_0$,而Bias是一个等于 $2^{k-1}-1$(单精度是127,双精度是1023)的偏置值。所以由此产生的指数的取值范围,对于单精度来说是 $-126 \thicksim +127$,对于双精度来说是 $-1022 \thicksim +1023$。
小数字段 $frac$ 被解释为描述小数值 $f$, 其中 $0\leqslant f < 1$,其二进制表示为 $0.f_{n-1}\cdots f_1f_0$,也就是二进制小数点在最高有效位的左边。尾数定义为 $M=1+f$。我们可以把 $M$ 看成是一个 $1.f_{n-1}f_{n-2}\cdots f_0$ 的数字。因为总是能够通过调整阶码 $E$ 使得尾数 $M$ 的值在范围 $1\leqslant M < 2$ 中,所以这一位可以省去,只保留后面的小数位,这样又能够获得一个精度位。
非规格化的值
当阶码位全为0时,表示的数就是非规格化的形式。这种情况下,阶码的值是 $E=1-Bias$,而尾数的值是 $M=f$,也就是小数字段的值不包括开头的1。
非规格化数有两个用途。
- 它们提供了一种表示数值0的方法,因为使用规格化数时,必须总是使 $M\geqslant 1$,这样就不能表示0。实际上,$+0.0$ 的浮点表示的位模式为全0:符号位是0,阶码字段全为0(表示是一个非规格化的值),而小数域也全为0,这就得到 $M=f=0$。但当符号位为1,其他域全为0时,会得到 $-0.0$。根据IEEE的浮点格式,值 $+0.0$ 和 $-0.0$在某些方面被认为是不同的,而在其他方面是相同的。
- 另外一个功能是表示哪些非常接近于 $0.0$ 的数。它们提供了一种属性,称为逐渐溢出(gradual underflow),其中,可能的数值分布均匀地接近于 $0.0$。
特殊值
这种情况是当阶码全为1时出现的。当小数域全为0时,得到的值表示无穷,当 $s=0$ 时是 $+\infty$,或者当$s=1$ 时是 $-\infty$。当把两个非常大的数相乘,或者除以0时,无穷可以表示溢出的结果。当小数域为非零时,结果值被称为 “NAN”。
下面想一下,为什么阶码的值要表示为 $E=e-Bias$?
下面内容参考自:https://www.zhihu.com/question/24115452
想一想,我们对两个用科学记数法表示的数进行加减法的时候,我们怎么做最简单?通过比较exponent的大小,然后通过移动小数点,让它们一致,之后,把数值部分相加,即可。
同样的,在计算机硬件的实现上,也是这样处理浮点数的加减法的~也就是通常所说的:求阶差、对阶,尾数相加,结果规格化。那么,这就产生了一个问题:如何比较两个阶的大小,以右移小阶所对应的fraction呢?
在原码的情况下,这样的比较是不方便的!因为按照规定,对于负数,符号位是1;正数,符号位是0。
那么一个正数01xxx和另一个正数00xxx比较,显然,01xxx大。
但是,一个正数0xxx和一个负数1xxx比较,还是按照上面的比较的话,我们认为是1xxx那个大。
所以,为了一个比较设计不同的电路确实不划算,所以让负数都变成正数,这样一来,比较就变得容易了。
舍入
因为表示方法限制了浮点数的范围和精度,所以浮点运算只能近似地表示实数运算。因此,对于值 $x$,我们一般想用一种系统的方法,能够找到“最接近的”匹配值 $x^\prime$,它可以用期望的浮点形式表示出来。这就是舍入运算的任务。
如果一个数是1.5,那么舍入到最接近的值应该是1还是2呢?下面介绍一下向偶舍入(round-to-even),也被称为向最接近的值舍入(round-to-nearest),这是默认的方式,方法是:它将数字向上或者向下舍入,使得结果的最低有效数字是偶数。因此,这种方法将1.5和2.5都舍入为2。
下面的表格用来说明舍入的方式:
| 方式 | 1.40 | 1.60 | 1.50 | 2.50 | -1.50 |
|---|---|---|---|---|---|
| 向偶舍入 | 1 | 2 | 2 | 2 | -2 |
| 向零舍入 | 1 | 1 | 1 | 2 | -1 |
| 向下舍入 | 1 | 1 | 1 | 2 | -2 |
| 向上舍入 | 2 | 2 | 2 | 3 | -1 |
为什么要使中间值向偶舍入呢?因为使用向上舍入或者向下舍入,会在计算这些值的平均数中引入统计偏差。如果两个数的中间值始终用向上舍入,那么得到的一组数的平均值将比这些数本身的平均值略高一些;相反,向下舍入得到的一组数的平均值将比这些数本身的平均值略低一些。
向偶舍入在大多数情况中避免了这种统计偏差,在 50% 的时间里,它将向上舍入,而在 50% 的时间里,它将向下舍入。
小数也可以使用向偶舍入,这时只需要考虑最低有效数字是奇数还是偶数。例如,假设想将十进制数舍入到最接近的百分位,不管用哪种舍入方式,我们都会将 1.2349999 舍入到 1.23,将 1.23450001 舍入到 1.24,因为它们都不是在 1.23 和 1.24 的正中间。如果是向偶舍入,则 1.2350000 和 1.2450000,因为 4 是偶数。
向偶舍入也可以使用在二进制小数上。我们将最低有效位的值0认为是偶数,值1认为是奇数。一般来说,只有对形如 $XX\cdots X.YY\cdots Y100\cdots$ 的二进制位模式的数,这种舍入方式才有效,其中 $X$ 和 $Y$ 表示任意位值,最右边的 $Y$ 是要被舍入的位置。只有这种位模式表示在两个可能的结果正中间的值。
例如,考虑舍入值到最近的四分之一(也就是二进制小数点右边2位)的位置时,我们将 $10.00011_2\left(2\frac3 {32}\right)$ 向下舍入到 $10.00_2(2)$, $10.00110_2\left(2\frac3 {16}\right)$ 向上舍入到 $10.01_2\left(2\frac1 {4}\right)$,因为这些值不是两个可能值的正中间值。我们将 $10.11100_2\left(2\frac7 {8}\right)$ 向上舍入为 $11.00_2(3)$,而 $10.10100_2\left(2\frac5 {8}\right)$ 向下舍入为 $10.10_2\left(2\frac5 {8}\right)$,因为这些值是两个可能值的中间值,并且我们倾向于使最低有效位为零。
为什么 $XX\cdots X.YY\cdots Y100\cdots$ 类型的数表示两个可能结果的中间值呢?以上面的例子说明,$10.11100_2$ 就是一个中间值,因为要保留到小数点后两位,所以看最后的 $100$,如果按照二进制整数来看的话,该值是十进制的4,而3位的二进制最大可以表示十进制中的7,可见4就是1到7的中间值了。
Double类的一些重要常量
下面看一下java中的Double类中定义的一些重要的常量:
|
|
通过上面的分析,理解这里定义的这些常量也就很容易了。